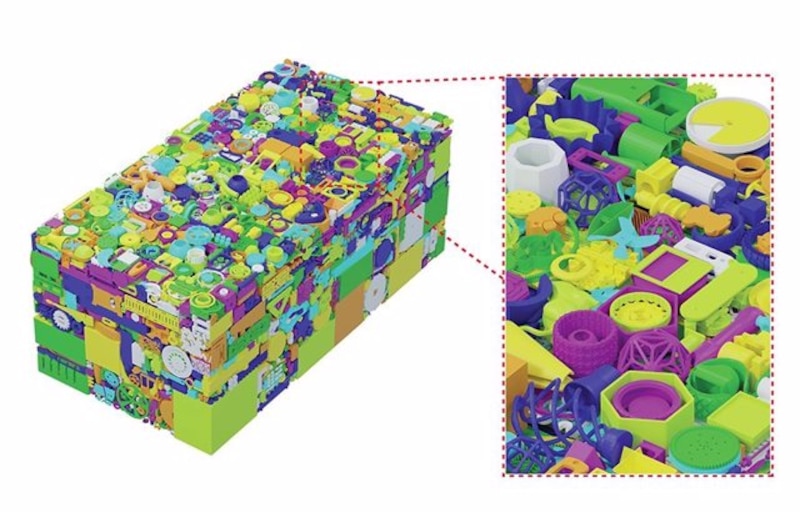
Un equipo dirigido por el MIT ha desarrollado un novedoso algoritmo para encontrar ubicaciones a objetos dentro de un contenedor y conseguir un empaquetado más rápido y fácil.
En 1611, Johannes Kepler, conocido por sus leyes del movimiento planetario, ofreció una solución a la pregunta sobre la forma más densa posible de disponer esferas del mismo tamaño. El famoso astrónomo abordó este problema cuando se le preguntó cómo apilar balas de cañón para que ocupen la menor cantidad de espacio. Kepler llegó a la conclusión de que la mejor configuración es la llamada red cúbica centrada en las caras, un enfoque que se usa comúnmente en las tiendas de comestibles para exhibir naranjas: cada bala de cañón debe descansar en la cavidad dejada por las cuatro balas de cañón (alineadas en un espacio apretado de dos por -dos cuadrados) que se encuentran directamente debajo de él. Sin embargo, esto era simplemente una conjetura que no fue probada hasta casi 400 años después por un matemático de la Universidad de Michigan.
Si bien eso resolvió el problema del empaquetado uniforme de las esferas, el problema más general, relacionado con la forma óptima de colocar objetos 3D de varios tamaños y formas, sigue sin resolverse. Este problema, de hecho, se clasifica como NP-difícil, lo que significa que no se puede resolver exactamente, ni siquiera aproximadamente, con un alto grado de precisión, sin requerir tiempos de cálculo absurdamente largos que podrían llevar años o décadas, dependiendo de la cantidad de piezas que deben encajar en un espacio confinado.
Sin embargo, ha habido un gran progreso, no en la forma de una prueba matemática, sino a través de una nueva metodología computacional que hace que esta tarea que antes era difícil de manejar sea más manejable.
Un equipo de investigadores del MIT e Inkbit (una empresa derivada del MIT con sede en Medford, Massachusetts), encabezado por Wojciech Matusik, profesor del MIT y cofundador de Inkbit, presenta esta técnica, a la que denominan "dense, interlocking-free and Scalable Spectral Packing" o SSP, en SIGGRAPH 2023, la conferencia más grande del mundo sobre gráficos por computadora y técnicas interactivas. Un documento se publicará el próximo mes en la revista ACM Transactions on Graphics.
El primer paso en SSP es elaborar un pedido de objetos 3D sólidos para llenar un contenedor fijo. Un enfoque posible, por ejemplo, es comenzar con los objetos más grandes y terminar con los más pequeños. El siguiente paso es colocar cada objeto en el contenedor. Para facilitar este proceso, el contenedor está "voxelizado", lo que significa que está representado por una cuadrícula 3D compuesta de pequeños cubos o vóxeles, cada uno de los cuales puede tener solo un milímetro cúbico de tamaño. La cuadrícula muestra qué partes del contenedor, o qué vóxeles, ya están llenos y cuáles están vacíos.
El objeto a envasar también se voxeliza, nuevamente representado por una aglomeración de cubos que tienen el mismo tamaño que los del contenedor. Para calcular el espacio disponible para este objeto, el algoritmo calcula una cantidad llamada métrica de colisión en cada vóxel. Funciona colocando el centro del objeto en cada vóxel del contenedor y luego contando el número de vóxeles ocupados con los que el objeto se superpone o "choca". El objeto solo se puede colocar en ubicaciones donde la superposición sea cero; en otras palabras, donde no haya colisiones.
El siguiente paso es analizar todas las ubicaciones posibles y determinar la mejor posición disponible para colocar el objeto. Para esta tarea, los investigadores calculan otra métrica en cada vóxel, que está diseñada para maximizar localmente la densidad de empaquetamiento. Esta métrica mide los espacios entre el objeto y la pared del contenedor, o entre el objeto que se está moviendo y los objetos que ya se encuentran dentro del contenedor. Si el objeto se coloca en el centro, por ejemplo, la métrica probablemente asignaría un valor alto.
Sin embargo, el objetivo es minimizar los espacios entre los objetos, y eso se puede lograr colocando el objeto donde el valor métrico es el más bajo. "Es como el juego Tetris", explica Matusik en un comunicado. "Quieres dejar el menor espacio vacío posible".
Copyright © 2023 La Crónica de Hoy .

